9.5 组合逻辑电路

组合逻辑电路：在任何时刻的输出状态只取决于这一时刻的输入状态，而与电路的原来状态无关的电路。

生活中组合电路的实例（电子密码锁，银行取款机等）

电路结构：由逻辑门电路组成。

电路特点：没有记忆单元，没有从输出反馈到输入的回路。

9.5.1组合逻辑电路的分析方法

提问：

1.描述组合逻辑电路逻辑功能的方法主要有？

 （逻辑表达式、真值表、卡诺图和逻辑图等。）

2.各种表示法之间的相互转换？

  组合逻辑电路的分析与设计相当于是各种表示法之间的相互转换。

一、基本分析方法

分析：给定逻辑电路→逻辑功能。

步骤：

1．给定逻辑电路→输出逻辑函数式

一般从输入端向输出端逐级写出各个门输出对其输入的逻辑表达式，从而写出整个逻辑电路的输出对输入变量的逻辑函数式。必要时，可进行化简，求出最简输出逻辑函数式。

2．列真值表

将输入变量的状态以自然二进制数顺序的各种取值组合代入输出逻辑函数式，求出相应的输出状态，并填入表中，即得真值表。

3．分析逻辑功能

通常通过分析真值表的特点来说明电路的逻辑功能。

二、分析举例

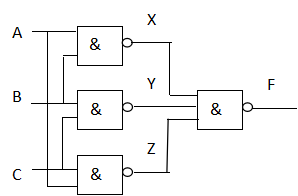
试分析图示组合逻辑电路的逻辑功能

（1）由逻辑图写出逻辑表达式，并化简

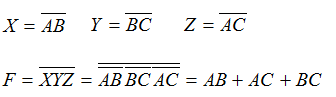
（2）列出真值表

 （3）分析逻辑功能

  当A、B、C中有两个或三个为1时，输出F为1；否则输出为0。

归纳总结：

 1.各步骤间不一定每步都要，如：省略化简（本已经成为最简）由表达式直接概述功能，不一定列真值表。

 2.不是每个电路均可用简炼的文字来描述其功能。 如Y=AB CD

9.5.2 组合逻辑电路的设计方法

一、基本设计方法

设计：设计要求→逻辑图。

步骤（与分析相反）:

 1．分析设计要求→列真值表

   根据题意设输入变量和输出函数并逻辑赋值，确定它们相互间的关系，然后将输入变量以自然二进制数顺序的各种取值组合排列，列出真值表。

 2．根据真值表→写出输出逻辑函数表达式

 3．对输出逻辑函数进行化简(代数法或卡诺图法)

 4．根据最简输出逻辑函数式→画逻辑图。

最简与一或表达式、与非表达式、或非表达式、与或非表达式、其它表达式

二、设计举例

例：设A、B、C为某保密锁的3个按键，当A键单独按下时锁既不打开也不报警；只有当A、B、C或者A、B或者A、C分别同时按下

    时锁才能打开；当不符合上述组合状态时，将发出报警信号。试用与非门设计此保密锁的逻辑电路。

解：（1）进行逻辑规定

   设三个按键按下为1，不按为0.设F和G分别为开锁信号和报警信号，开锁为1，不开锁为0；报警为1，不报警为0.

（2）列真值表

（2）求最简逻辑表达式

     利用卡诺图可得

（3）变换为与非式,画逻辑电路图

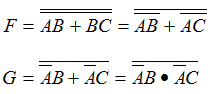
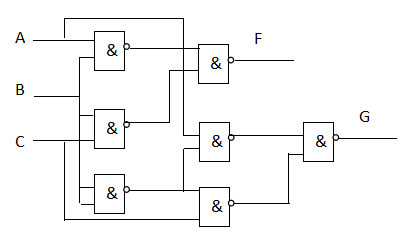
小结

   本节主要学习的是组合逻辑电路的设计和分析方法，需要重点掌握。