9.2 基本逻辑门电路及应用

一、概述

布尔：英国数学家，1941年提出变量“0”和“1”代表不同状态。
本章主要介绍逻辑代数的基本运算、基本定律和基本运算规则，然后介绍逻辑函数的表示方法及逻辑函数的代数化简法和卡诺图化简法。逻辑代数有其自身独立的规律和运算法则，而不同于普通代数。

逻辑函数及其表示法

二、基本逻辑函数及运算

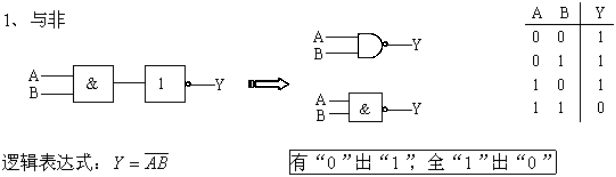
1、与运算 ——— 所有条例都具备事件才发生

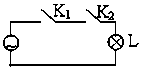
开关：“1” 闭合，“0” 断开

灯：“1” 亮，“0” 灭

真值表：把输入所有可能的组合与输出取值对应列成表。

逻辑表达式： L=K1*K2 (逻辑乘)

逻辑符号：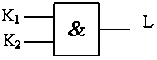 

逻辑功能口决： 有“0”出“0”，全“1”出“1”。

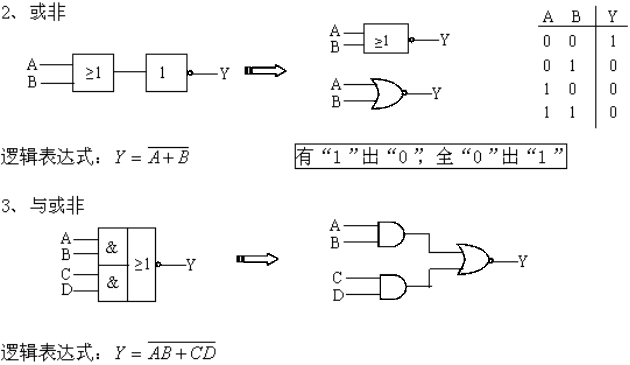
2、或运算 ——— 至少有一个条件具备，事件就会发生。     

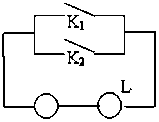
逻辑表达式：L=K1 K2 （逻辑加）

逻辑符号：

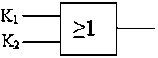
逻辑功能口决：有“1”出“1”全“0”出“0”

3、非运算： — 结果与条件相反

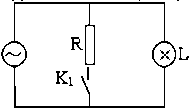
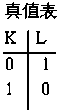
逻辑表达式： 

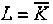
逻辑符号：

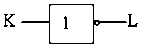
三、几种导出的逻辑运算

逻辑表达式：   相同为“1”，不同为“0”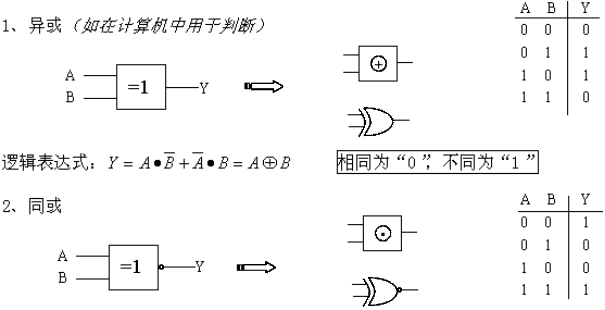

逻辑表达式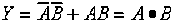：   相同为“1”，不同为“0”

四、逻辑代数的基本定律和规则

变量A的取值只能为0或为1，分别代入验证。

逻辑代数的基本定律

  逻辑代数的基本定律是分析、设计逻辑电路，化简和变换逻辑函数式的重要工具。                           

第④式的推广： 

由表2.3.4可知，利用吸收律化简逻辑函数时，某些项或因子在化简中被吸收掉，使逻辑函数式变得更简单。

三、摩根定律

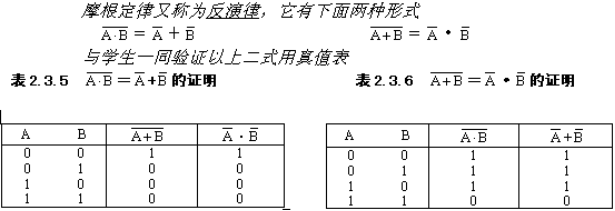
逻辑代数的三个重要规则

一、代入规则

对于任一个含有变量A的逻辑等式，可以将等式两边的所有变量A用同一个逻辑函数替代，替代后等式仍然成立。这个规则称为代入规则。代入规则的正确性是由逻辑变量和逻辑函数值的二值性保证的。

若两函数相等，其对偶式也相等。 （可用于变换推导公式）。

小结

    本节主要介绍了三种基本的逻辑关系及导出的复合逻辑关系，并讲解了逻辑运算的规则