9.4 逻辑涵数的化简

（一）化简逻辑函数的意义

    根据逻辑问题归纳出来的逻辑函数式往往不是最简逻辑函数式，对逻辑函数进行化简和变换，可以得到最简的逻辑函数式和所需要的形式，设计出最简洁的逻辑电路。这对于节省元器件，优化生产工艺，降低成本和提高系统的可靠性，提高产品在市场的竞争力是非常重要的。

（二）逻辑函数的代数化简法

一、并项法 

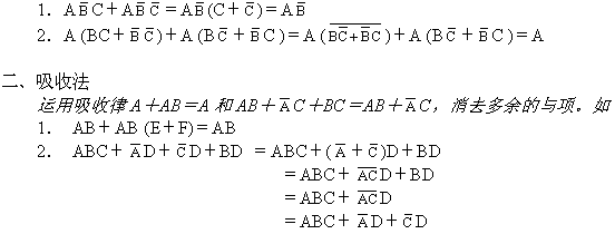
（三）逻辑函数的卡诺图化简法

步骤：

      ①画卡诺图 ②正确圈组 ③写最简与或表达式

画包围圈时应遵循的原则：

     （1）包围圈内的方格数一定是2n个，且包围圈必须呈矩形。

     （2）循环相邻特性包括上下底相邻，左右边相邻和四角相邻。

     （3）同一方格可以被不同的包围圈重复包围多次，但新增   的包围圈中一定要有原有包围圈未曾包围的方格。

     （4）一个包围圈的方格数要尽可能多,包围圈的数目要尽可能少。

[例]：用卡诺图将下式化简为最简与-或逻辑函数式。

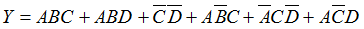
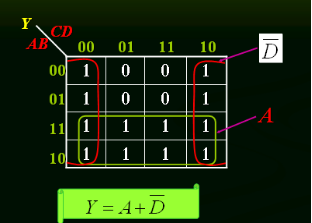
   具有无关项的逻辑函数的化简

一、 
逻辑函数中的无关项

  用“×”（或“d” ）表示

  利用无关项化简原则：

  ① 无关项即可看作“1”也可看作“0”。

  ② 卡诺图中，圈组内的“×”视为“1”，圈组外的视为“0”。

  例2. 5. 6 为8421BCD码，当其代表的十进制数≥5时，输出为“1”，求Y的最简表达式。（用于间断输入是否大于5）

  解：先列真值表，再画卡诺图

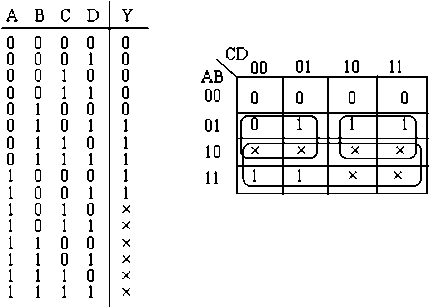
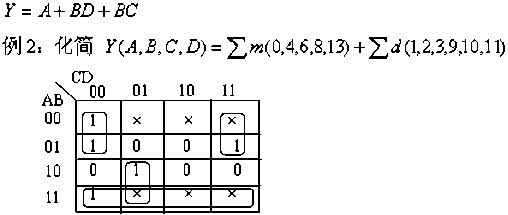
小结

    本节主要介绍了最小项的定义和性质、用卡诺图表示逻辑函数的方法及运用卡诺图化简逻辑函数的方法，重点掌握运用卡诺图化简函数的方法。