9.1数制与编码

9.1.1 数制

基数：一种数制所具有的数码个数

权：不同位置上数码的单位数值

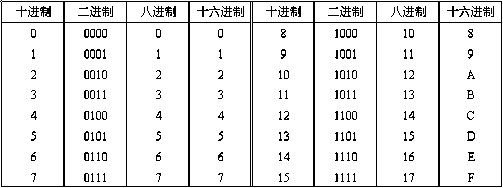
不同数制间的转换

一、各种数制转换成十进制

二进制、八进制、十六进制转换成十进制时，只要将它们按权展开，求出各加权系数的和，便得到相应进制数对应的十进制数。

例：

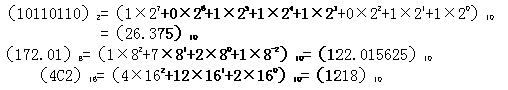
二、十进制转换为二进制

将十进制数的整数部分转换为二进制数采用“除2取余法”；

将十进制小数部分转换为二进制数采用“乘2取整法”。

例：将十进制数(107.625)10转换成二进制数。

解：① 整数部分转换

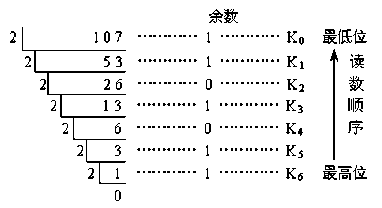
所以，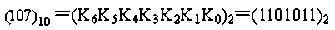

②小数部分转换

将十进制小数部分转换为二进制数采用“乘2取整法”，它是将小数部分连续乘以2，取乘数的整数部分作为二进制数的小数。

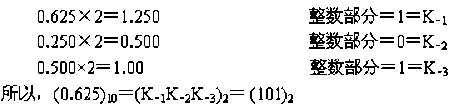
由此可得十进制数(107.625)10对应的二进制数为  (107.625)10＝(1101011.101)2

三、二进制与八进制、十六进制间相互转换

1．二进制和八进制间的相互转换

（1） 二进制数转换成八进制数。

    二进制数转换为八进制数的方法是：整数部分从低位开始，每三位二进制数为一组，最后不足三位的，则在高位加0补足三位为止；小数点后的二进制数则从高位开始，每三位二进制数为一组，最后不足三位的，则在低位加0补足三位，然后用对应的八进制数来代替，再按顺序排列写出对应的八进制数。

例：将二进制数(11100101.11101011)2转换成八进制数。

(11100101.11101011)2＝(345.726)8

（2） 八进制数转换成二进制数。

    将每位八进制数用三位二进制数来代替，再按原来的顺序排列起来，便得到了相应的二进制数。

例：将八进制数(745.361)8转换成二进制数。

(745.361)8＝ (111100101.011110001)2

2．二进制和十六进制间的相互转换

（1） 二进制数转换成十六进制数。

    二进制数转换为十六进制数的方法是：整数部分从低位开始，每四位二进制数为一组，最后不足四位的，则在高位加0补足四位为止；小数部分从高位开始，每四位二进制数为一组，最后不足四位的，在低位加0补足四位，然后用对应的十六进制数来代替，再按顺序写出对应的十六进制数。

例： 将二进制数(10011111011.111011)2转换成十六进制数。

(10011111011.111011)2＝(4FB.EC)16

（2）十六进制数转换成二进制数。

将每位十六进制数用四位二进制数来代替，再按原来的顺序排列起来便得到了相应的二进制数。

例：将十六进制数(3BE5.97D)16转换成二进制数。

(3BE5.97D)16＝(11101111100101.100101111101)2

6.1.2 编码

一、二-十进制代码

将十进制数的0～9十个数字用二进制数表示的代码，称为二-十进制码，又称BCD码。

常用二-十进制代码表（重点讲解8421码、5421码和余3码）

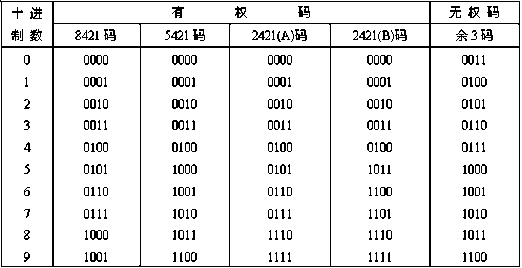
                                 注意：含权码的意义。

8421码各位的权从左到右分别为8、4、2、1。

余3码是由8421码加3（0011）得来的，是一种无权码。

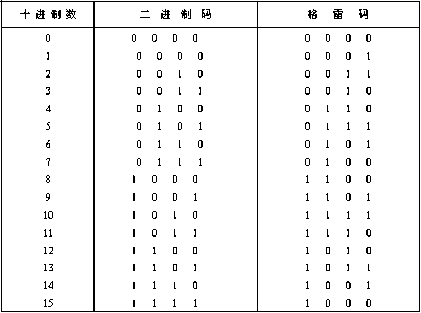
格雷码的特点是从一个代码变为相邻的另一个代码时只有一位发生变化。

缺点是与十进制数之间不存在规律性的对应关系，不够直观。

小结：

   本节主要介绍了数字信号和数字电路的基本知识，重点介绍了编码和数制，重点掌握数制之间的转换和各种编码的特点。