9.3 逻辑函数及其表示法

一、逻辑函数的建立

举例子说明建立（抽象）逻辑函数的方法，加深对逻辑函数概念的理解。

例 两个单刀双掷开关 A和B分别安装在楼上和楼下。上楼之前，在楼下开灯，上楼后关灯；反之下楼之前，在楼上开灯，下楼后关灯。试建立其逻辑式。

真值表

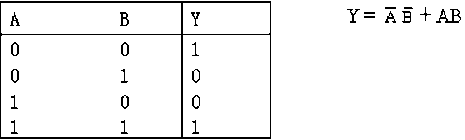
二、逻辑函数的表示方法

1．真值表

逻辑函数的真值表具有唯一性。逻辑函数有n个变量时，共有 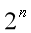个不同的变量取值组合。在列真值表时，变量取值的组合一般按n位二进制数递增的方式列出。用真值表表示逻辑函数的优点是直观、明了，可直接看出逻辑函数值和变量取值之间的关系。

分析逻辑式与逻辑图之间的相互转换以及如何由逻辑式或逻辑图列真值表。

2．逻辑函数式

写标准与-或逻辑式的方法是：

（l）把任意一组变量取值中的1代以原变量，0代以反变量，由此得到一组变量的与组合，如 A、B、C三个变量的取值为 110时，则代换后得到的变量与组合为 A B 。

（2）把逻辑函数值为1所对应的各变量的与组合相加，便得到标准的与-或逻辑式。

3．逻辑图

逻辑图是用基本逻辑门和复合逻辑门的逻辑符号组成的对应于某一逻辑功能的电路图。

最小项与卡诺图

一、最小项的定义和性质

1．最小项的定义

包含全部输入变量作为因子，每个变量以原变量或反变量形式必须出现且仅出现一次的乘积项

特点：每项都有n个变量

每个乘积中每个变量出现且仅出现1次

　2．最小项的基本性质

    a．只有一组取值使之为“1”

    b．任二最小项乘积与“0”

    c．所有最小项之和为“1”

二、表示最小项的卡诺图

  1．相邻最小项

     逻辑相邻项——只有一个变量取值不同其余变量均相同的最小项

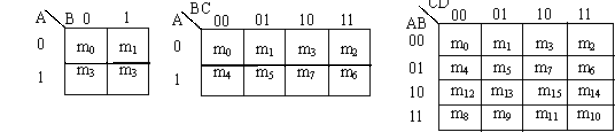
   两个相邻最小项可以相加合并为一项，同时消去互反变量，合并结果为相同变量。

   对于五变量及以上的卡诺图，由于很复杂，在逻辑函数的化简中很少使用。

  用卡诺图表示逻辑函数

 一、逻辑函数的标准与-或式

   如一个或逻辑式中的每一个与项都是最小项，则该逻辑式叫做标准与-或式，又称为最小项表达式，并且标准与-或式是唯一的。

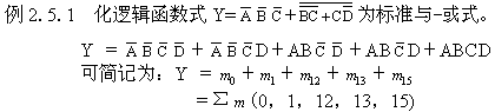
 二、用卡诺图表示逻辑函数

 1．最小项表达式 卡诺图

 例2. 5. 2 试画出例2. 5. 1中的标准与-或式的卡诺图。

 解：（1）画出4变量最小项卡诺图，如图2. 5. 4所示。

 2．真值表 卡诺图

逻辑函数真值表和逻辑函数的标准与-或式是—一对应的关系，所以可以直接根据真值表填卡诺图。

 3．一般表达式样 卡诺图

 (1)化为最小项表达式

 (2)把卡诺图中含有某个与项各变量的方格均填入1，直到填完逻辑式的全部与项。

小结

   本节主要介绍了逻辑函数的表示方法和代数法化简逻辑函数式，重点掌握逻辑函数式的代数化简法。