2.2  同频率正弦量的运算

2.2.1  正弦量的相量表示法

1. 相量

一个正弦量可以用三角函数式表示，也可以用正弦曲线表示。若用复数来表示正弦量，则可用复数的模来表示正弦量的幅值，用复数的幅角表示正弦量的初相。

实际使用中，往往采用有效值，即相量的模采用正弦量的有效值，如正弦电流i的有效值相量为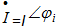

同样，电压、电动势均可利用相量表示。

需要注意，电流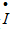相量、电压相量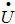等和瞬时值一样，可以在电路图上标出参考方向，而交流有效值I、U或最大值I_m、U_m等只有数值的大小。

2.相量图

相量和复数一样可以在复平面上用有向线段来表示，线段的长表示相量的模，线段与正实轴的夹角等于相量的幅角，这种表示相量的图形，称为相量图。

所谓相量图表示法，就是用一个在直角坐标系中用绕原点旋转的矢量表示正弦交流电的方法。

实际应用中也常采用有效值相量图，这样，相量图中每一个相量的长度不再是最大值，而是有效值，有效值相量用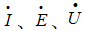表示。

2.2.2  相量的计算

在电路的分析计算中，往往需要把几个同频率的正弦量进行加、减运算。

用相量表示正弦交流电以后，它们的加、减运算就可以按平行四边形法则进行。

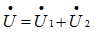
    小结：本节主要介绍了正弦交流电的基本知识，表示正弦交流电的方法及计算方法，重点掌握几种表示方法的转换和同频率正弦交流电的计算。