4.3  轴测图

     一、 概述

    1.轴测图的作用

     三面正投影图作图简便、度量性好，但是缺乏立体感，直观性很差，未经过专门训练的人很难看懂。
     轴测图是一种单面投影图，可以在一个投影面上同时反映形体的三维尺度，比较形象、逼真，很有立体感。但是由于轴测图作图复杂，并且度量性很差，很难准确反映形体的实际大小，一般只做辅助性图样。见下图：
   

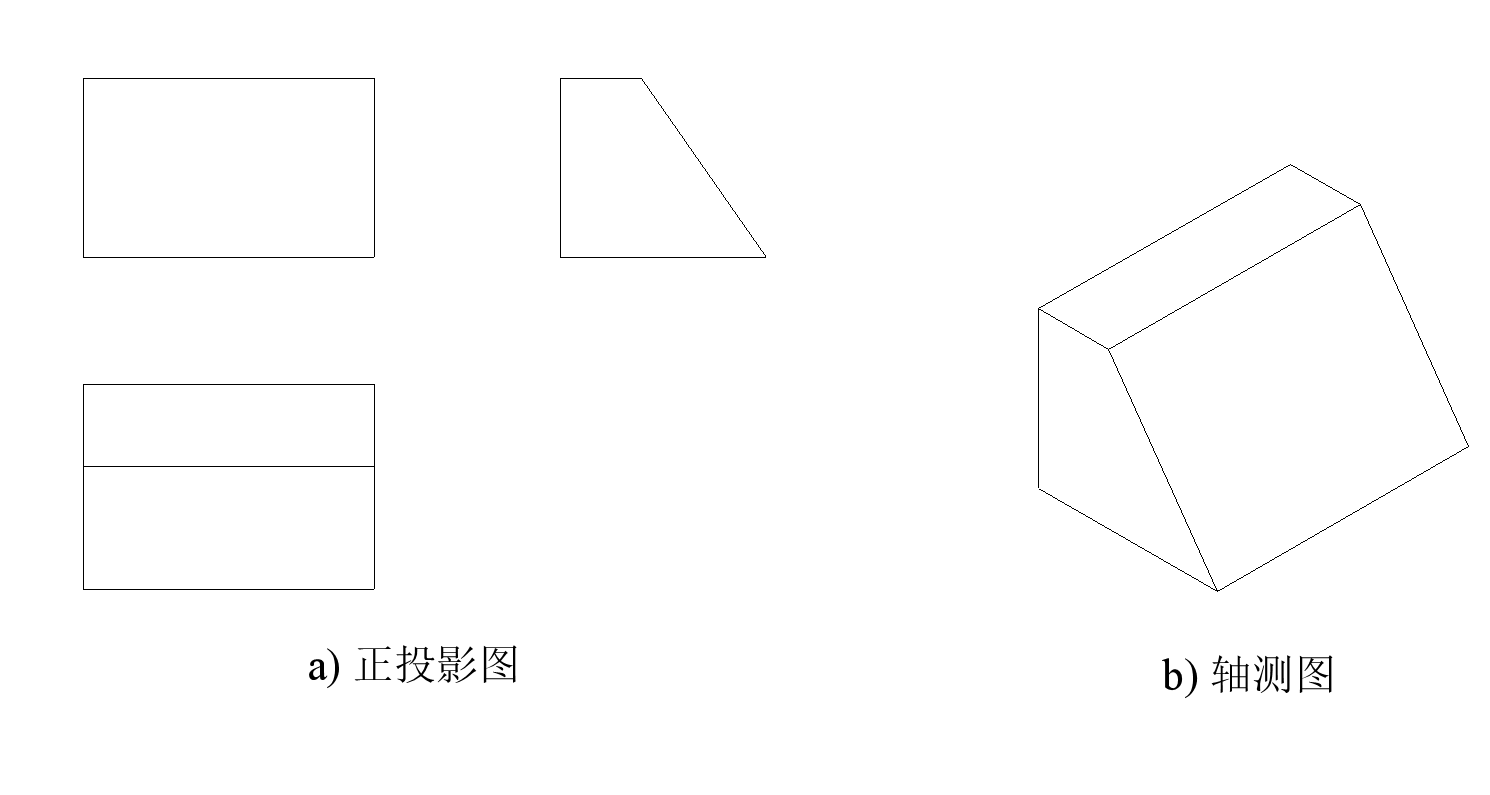
       2.轴测图的形成

    将形体连同确定它空间位置的直角坐标系一起，用平行投影法，沿不平行任一坐标面的方向S投射到一个投影面P上，所得到的投影称为轴测投影。用这种方法画出的图称为轴测投影图，简称轴测图。
     用平行投影法中的正投影法或斜投影法，把空间形体连同确定该形体的空间直角坐标系一起投影到一个投影面上，这样得到的图称为轴测投影图。

      3.轴测图的基本参数

      １）轴间角：轴测轴之间的夹角。如图中的∠X₁ O₁ Y₁、∠X1 O1 Z1、∠Z1 O1 Y1。
       2）轴向变形系数：轴测轴上某段长度与它的实长之比，称为轴向变形系数。
          常用字母p、q、r来分别表示OX、OY、OZ轴的轴向变形系数，可表示如下：
         OX轴的轴向变形系数  p= O1X1/OX
         OY轴的轴向变形系数  q= O1Y1/OY
         OZ轴的轴向变形系数  r= O1Z1/OZ
     4.轴测图的基本性质

     由于轴测图是根据平行投影原理绘制的，必然具备平行投影的一切特性。利用下面特性可以快速准确地绘制轴测投影图。
     1）平行性
       空间互相平行的线段，它们的轴测投影仍然互相平行。因此，形体上与坐标轴平行的线段，其轴测投影必然平行与相应的轴测轴，且其变形系数与相应的轴向变形系数相同。而空间不平行坐标轴的线段不具备该特性。

      2）定比性
     空间互相平行的两线段长度之比，等于它们的轴测投影长度之比。
      因此，形体上平行于坐标轴的线段，其轴测投影长度与实长之比，等于相应的轴向变形系数。另外，同一直线上的两线段长度之比，与其轴测投影长度之比也相等。

       3）显实性
      空间形体上平行于轴测投影面的直线和平面，在轴测图上反映实长和实形。因此，可选择合适的轴测投影面，使形体上的复杂图形与之平行，可简化做图过程。
       4）变形性
      凡形体上与坐标轴不平行的直线，其投影会缩短或变长，不能在图上直接量取，而要先定出直线两端点的位置，再画出该直线的轴侧投影。
     5.轴测图的分类

      （１）按投射方向分类
按照投射方向和轴测投影面相对位置的不同分为两类：
1) 正轴测投影图
  投射方向S垂直于轴测投影面时，可得到正轴测投影图，简称正轴测图。此时，三个坐标平面均不平行于轴测投影面。
2)斜轴测投影图
  投射方向S不垂直于轴测投影面时，可得到斜轴测投影图，简称斜轴测图。一般选一个坐标平面平行于轴测投影面，如选XOY坐标平面平行于轴测投影面可得到水平斜轴测投影图。
     （2）按轴向变形系数分类
在上述两类轴测投影图中，按照轴向变形系数的不同，  又有如下分类：
1）正轴测图
① 正等轴测图：p=q=r时，简称正等测。
② 正二等轴测图：p=q≠r时，或q=r≠p或p=r≠q时，简称正二测。
③ 正三等轴测图：p≠q≠r时，简称正三测。
2）斜轴测图
① 斜等轴测图：p=q=r时，简称斜等测。
② 斜二等轴测图：p=q≠r时，或q=r≠p或p=r≠q时，简称斜二测。
③ 斜三等轴测图：p≠q≠r时，简称斜三测。
    二、 正等轴测图
    1.正等轴测图的轴间角和轴向变形系数

    当投射方向S垂直于轴测投影面P，并且三个坐标轴的轴向变形系数均相等时，三个坐标轴与轴测投影面P倾角相等，投影三角形为等边三角形。
    根据几何知识，可以得到正等轴测图的轴向变形系数p=q=r=0.82，轴间角∠X1O1Y1=∠X1O1Z1=∠Z1 O1Y1=120°。
    为简化作图，习惯上把O1Z1轴画成铅垂位置，O1X1 轴和O1Y1轴均与水平线成30°角，可直接利用30°三角板作图。
     2．正等轴测图的常用画法

       正等轴测图的常用画法是坐标法、叠加法和端面法。在实际作图中，应根据形体特点的不同灵活采用。为了使图形清晰，作图时应尽量减少不必要的辅助线，一般先从可见部分作图。同时，要合理利用轴测图的特性，比如平行性等，来简化作图。
     （1）  坐标法
      正等轴测图的基本画法是坐标法，即先根据各点的坐标定出其投影，然后依次连线，再形成形体。
例1 如图（a）所示，已知某形体的两面正投影图，画出其正等轴测图。 

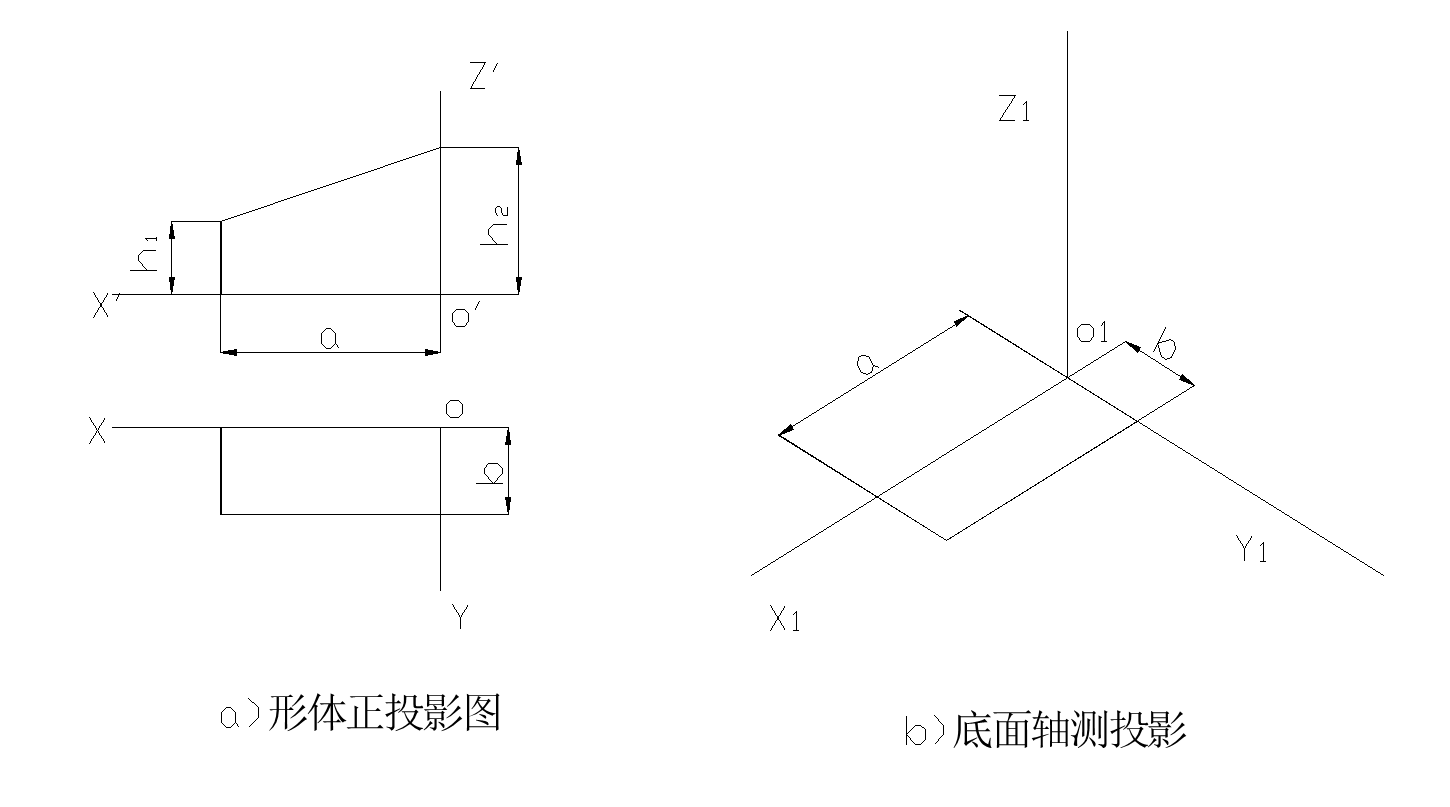
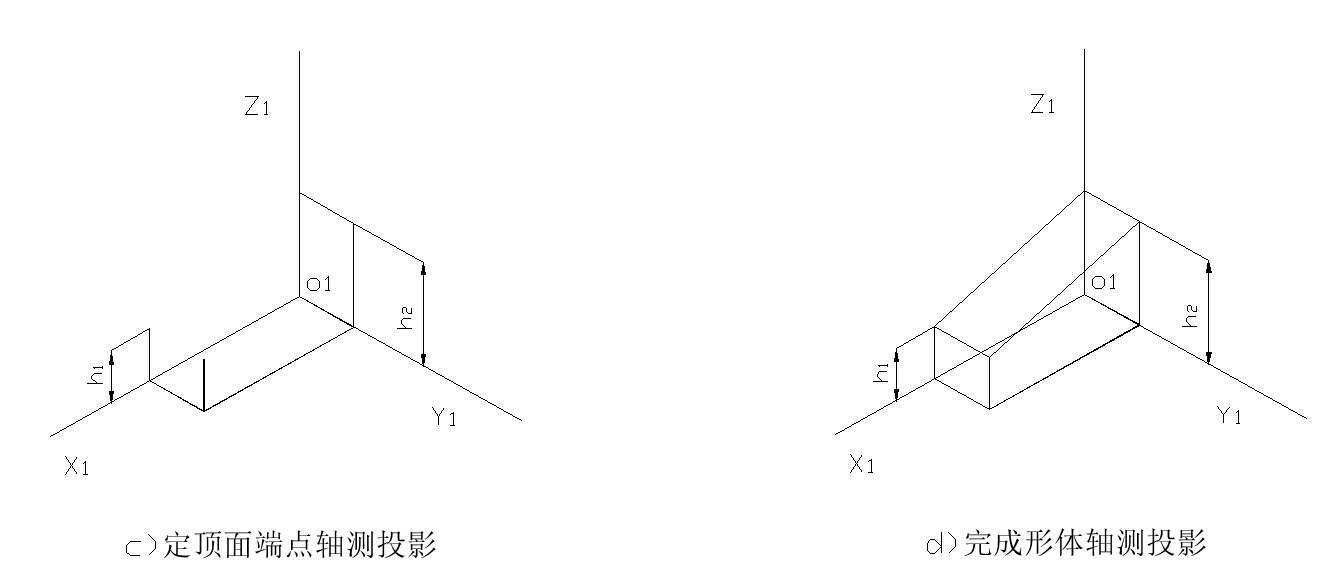
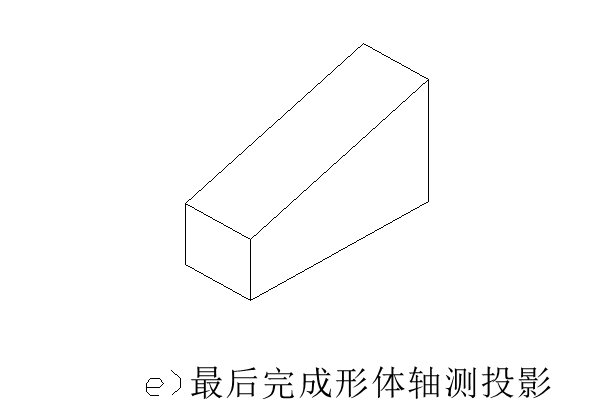
            （2）  叠加法

     组合形体可以看成由几个基本形体叠加而成，其正等测可以分解为几个基本形体的正等测，为便于作图，要注意各部分的相对关系，选择合适的顺序。
     例2：已知某形体的两面正投影图，画出其正等轴测图。

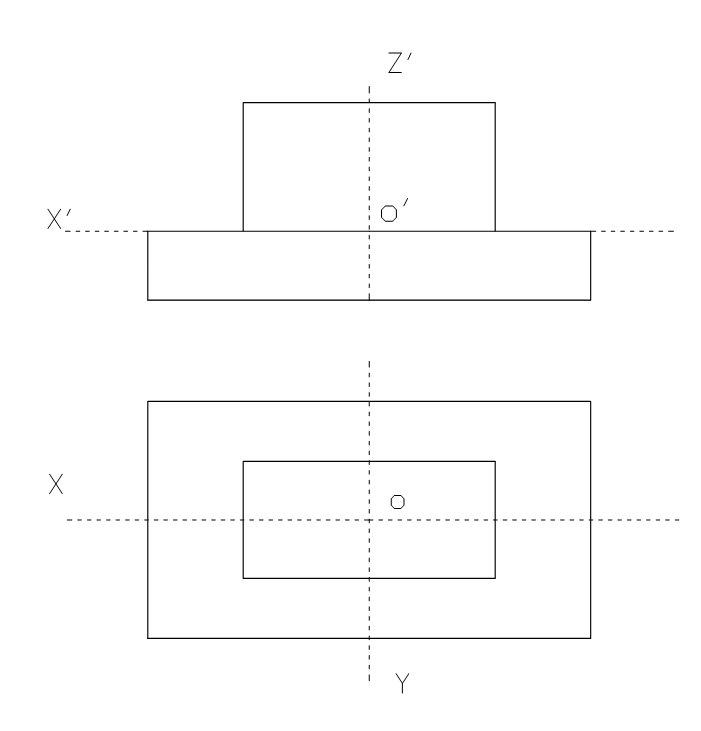
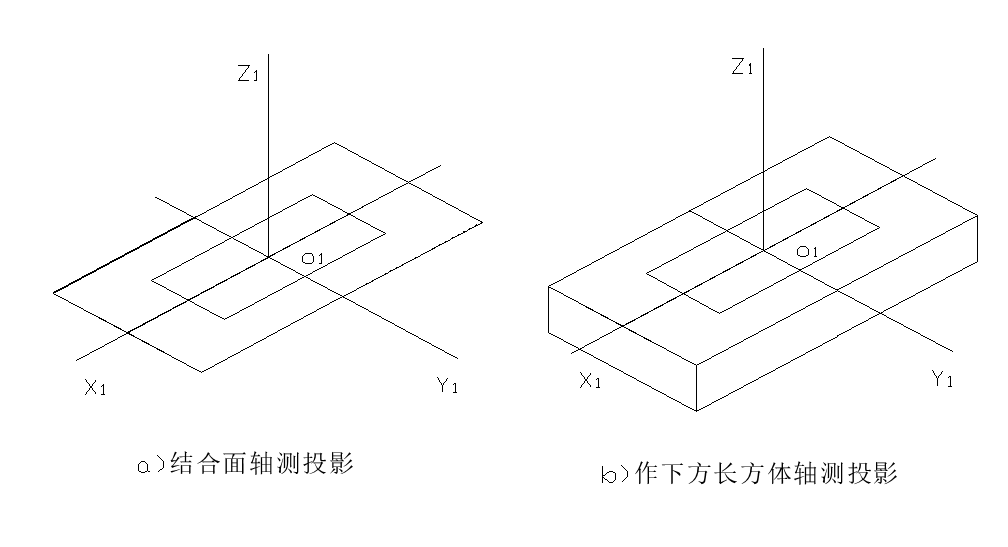
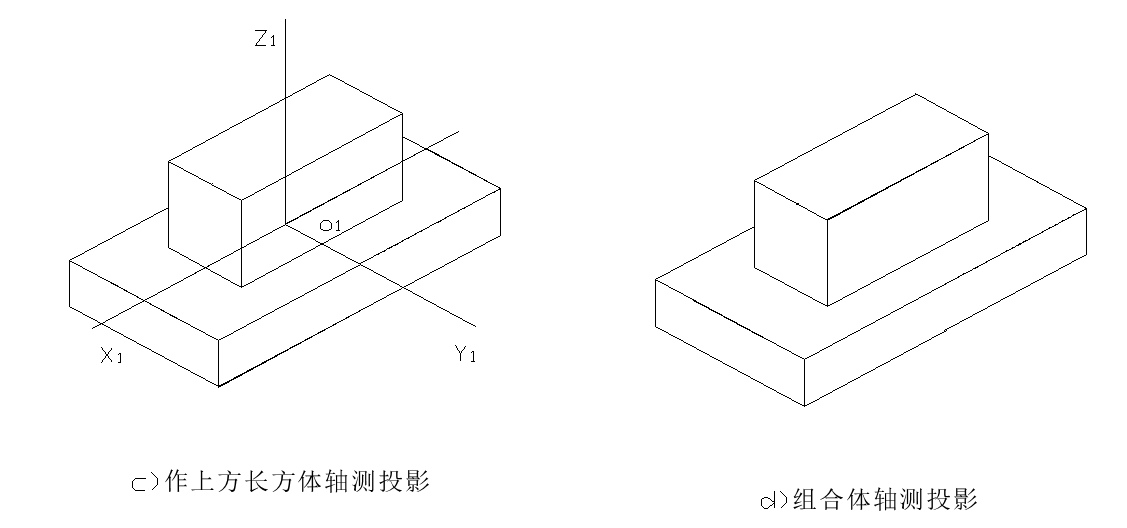
     解：首先想象空间形体，由投影图可知，该形体是由上下两个长方体叠加而成，两个长方体均为前后、左右对称。可选结合面中心为坐标原点建立坐标系，然后利用对称性，结合坐标法定出形体上下两底面的投影，相连即可。

    （3）  端面法

     一般先画出某一端面的正等测图，然后过该端面上各可见顶点，依次加上平行于某轴的高度或长度，得到另一端面上的各顶点，再依次连接即可。
    例3： 如图所示，已知台阶的两面正投影图，画出其正等轴测图。

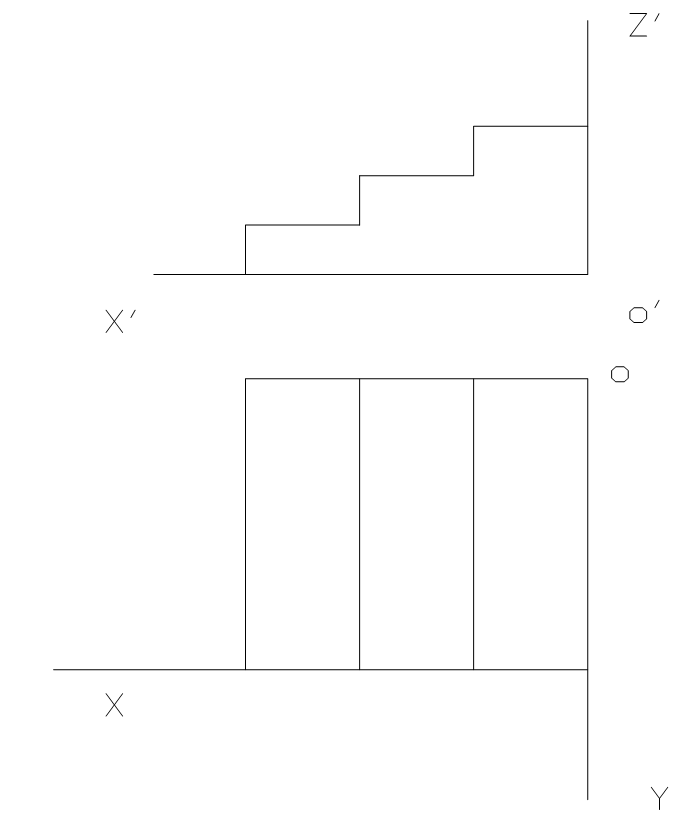
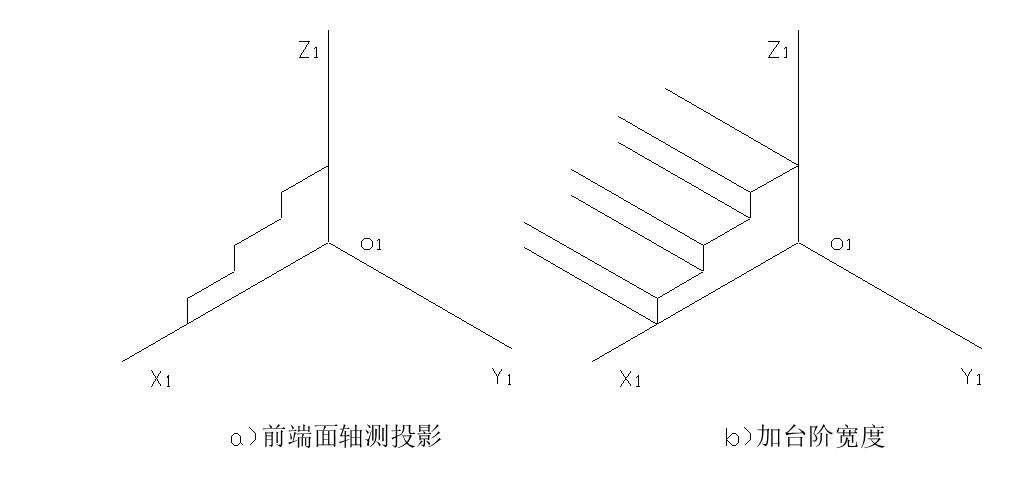
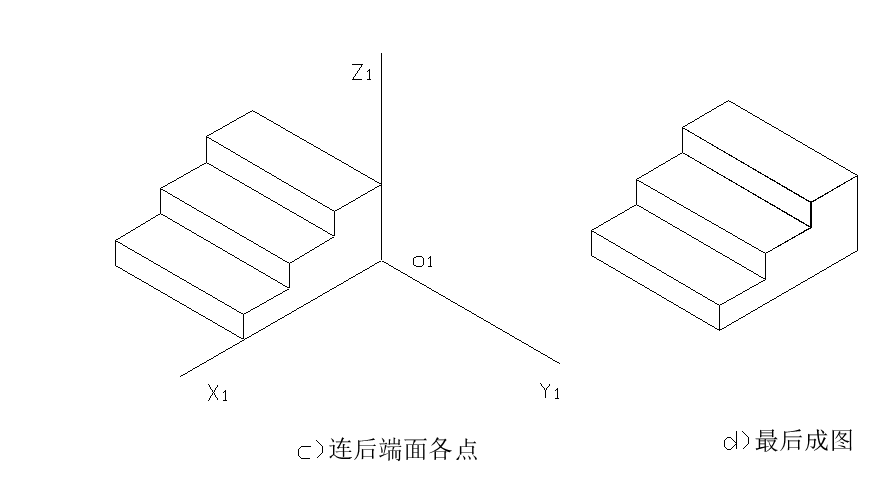
    3．圆的正等轴测图的画法
    以水平圆为例，介绍其正等轴测图的画法，过程如下：
    1）在已知正投影上，选定坐标原点和坐标轴，作出圆的外切正方形，定出外切正方形与圆的四个切点。
    2）画正等轴测轴，圆外切正方形的轴测投影。

    3）以o0为圆心，o0a1为半径作圆弧a1 b1；以o2为圆心，o2o1为半径作圆弧a1 b1。
    4）连接菱形长对角线，与o0a1交于o3，与o2c1交于o4。 以o3为圆心，o0d1为半径作圆弧d1a1；以o4为圆心，o4c1为半径作圆弧c1 b1。
     以四段圆弧组成的近似椭圆，即为所求圆的正等测投影。
      

        三、 斜二等轴测图

     当投射方向S倾斜于轴测投影面P，且两个坐标轴的轴向变形系数相等时，所得到的投影图是斜二等轴测投影图，简称斜二测。
     其中，当p=q≠r时，坐标面XOY平行于投影面P，得到的是水平斜二测；当p=r≠q时，坐标面XOZ平行于投影面P，得到的是正面斜二测。
     斜二测的轴间角和轴向变形系数
     当某坐标面平行于投影面P时，根据显实性，该坐标面的两轴投影仍垂直，且两个坐标轴的轴向变形系数恒为1。
    作图时，水平斜二测的轴间角和轴向变形系数常用值见图，一般取OZ轴为铅垂方向，OX轴和OY轴垂直，且OX与水平线成30°，45°或60°，为简化作图，常取r = 1，即有p=q =r = 1。
      

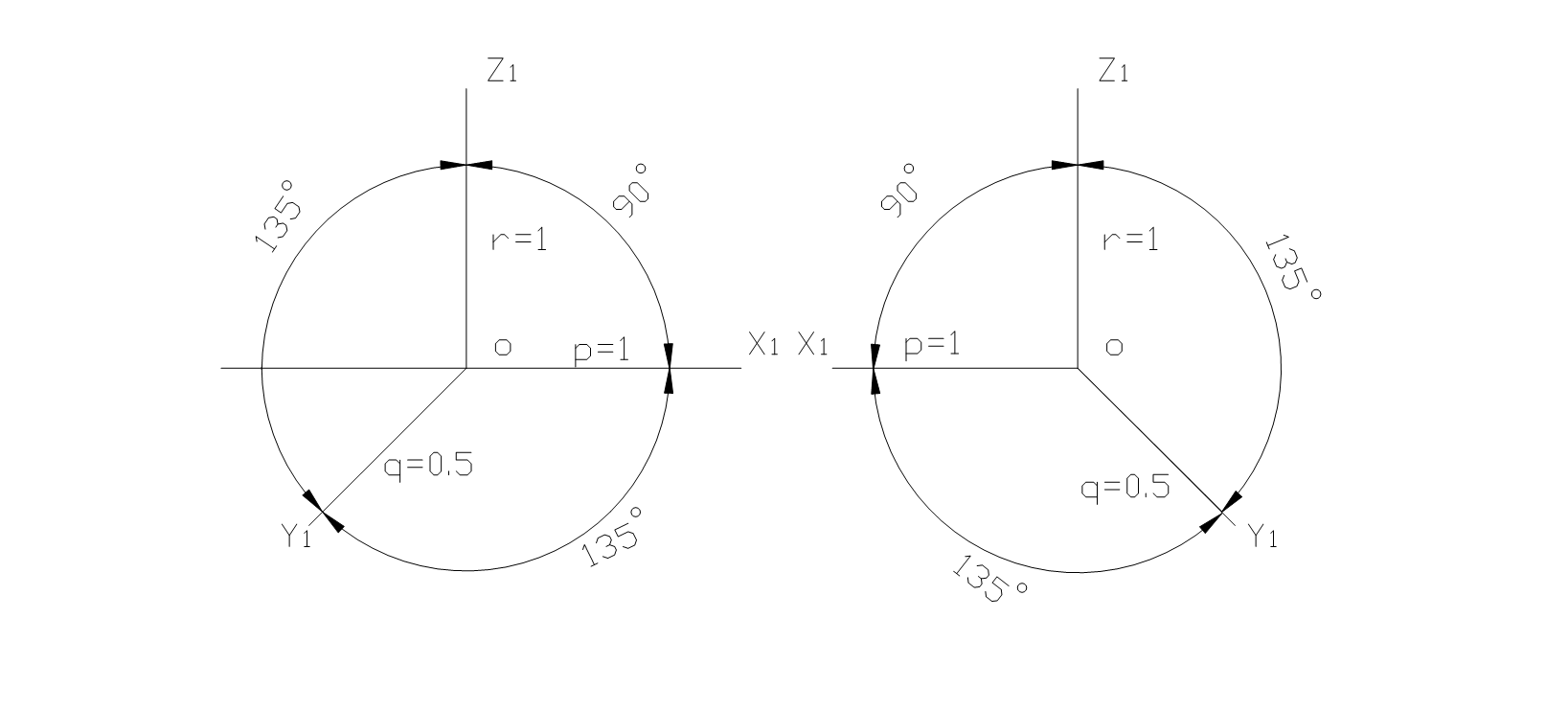
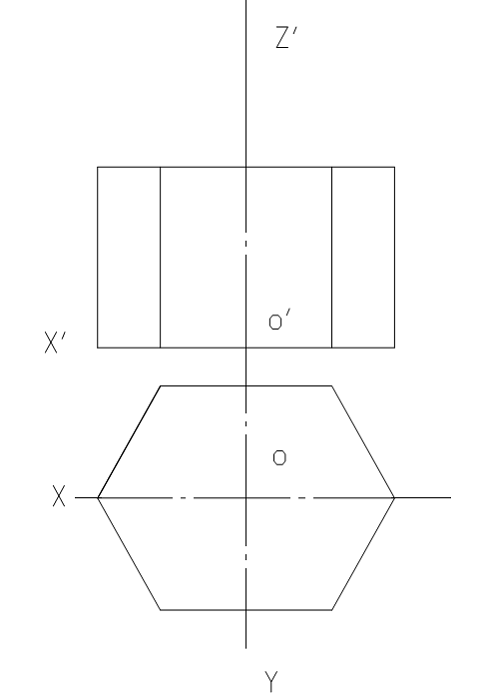
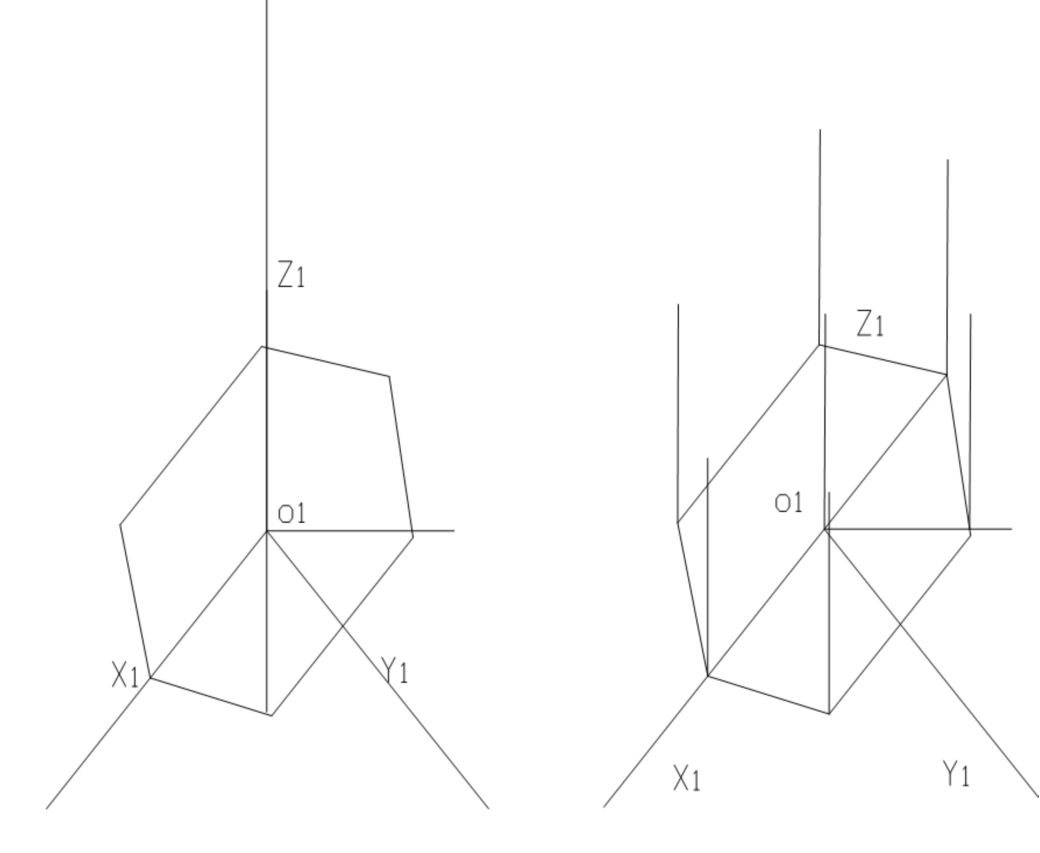
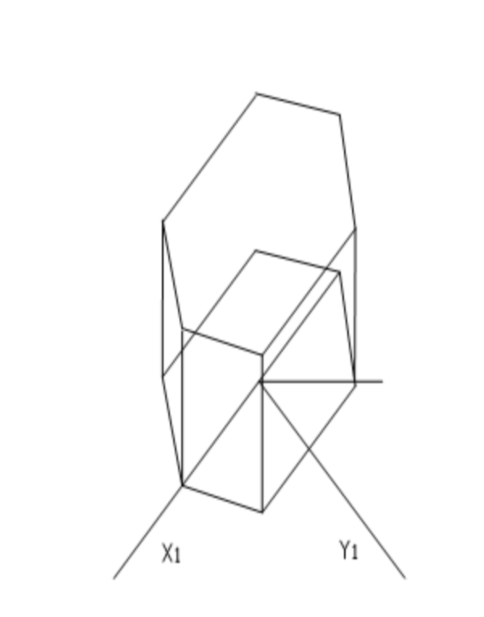
     例5：已知某棱台的两面正投影图，画出其水平斜二测图。

    解：首先想象空间形体。由投影图可知，该形体是一个六棱柱，可利用坐标法作图。根据题意，放置形体使下底面平行于水平面，得到六顶点的水平斜二测投影后，向上加上高度便可成图。