1.三角函数的符号

2.同角三角函数的关系（六边形记忆法）

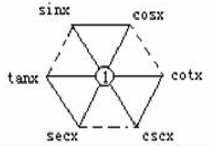
(1)倒数关系：对角线上两个函数互为倒数;

(2)乘积关系（相邻关系）：六边形任意一顶点上的函数值等于与它相邻的两个顶点上函数值的乘积。

(3)平方关系：在带有阴影线的三角形中，上面两个顶点上的三角函数值的平方和等于下面顶点上的三角函数值的平方。

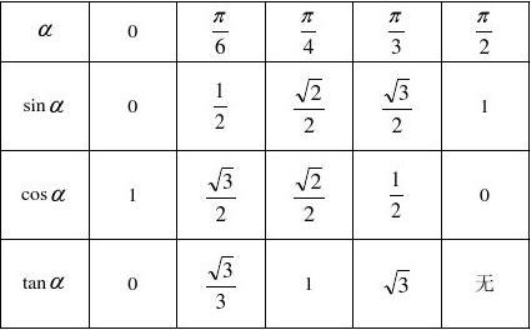
3.常用的三角函数值

（其他的用诱导公式等推导）

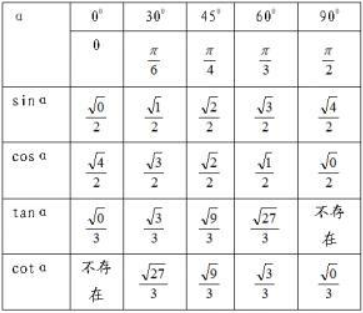
4.诱导公式

    诱导公式可以概括为（奇变偶不变，符号看象限）：

     对于π/2*k ±α(k∈Z)的三角函数值，

          ①当k是偶数时，得到α的同名函数值，即函数名不改变;

          ②当k是奇数时，得到α相应的余函数值，即sin→cos;cos→sin;tan→cot，cot→tan.

                        (奇变偶不变)

        然后在前面加上把α看成锐角时原函数值的符号。

                        (符号看象限)

    诱导公式一

　　设α为任意角，终边相同的角的同一三角函数的值相等：

　　sin(2kπ α)=sinα (k∈Z)

　　cos(2kπ α)=cosα (k∈Z)

　　tan(2kπ α)=tanα (k∈Z)

　　cot(2kπ α)=cotα (k∈Z)

    诱导公式二

　　设α为任意角，π α的三角函数值与α的三角函数值之间的关系：

　　sin(π α)=-sinα

　　cos(π α)=-cosα

　　tan(π α)=tanα

　　cot(π α)=cotα

    诱导公式三

　　任意角α与-α的三角函数值之间的关系：

　　sin(-α)=-sinα

　　cos(-α)=cosα

　　tan(-α)=-tanα

　　cot(-α)=-cotα

    诱导公式四

　　利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：

　　sin(π-α)=sinα

　　cos(π-α)=-cosα

　　tan(π-α)=-tanα

　　cot(π-α)=-cotα

    诱导公式五

　　利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：

　　sin(2π-α)=-sinα

　　cos(2π-α)=cosα

　　tan(2π-α)=-tanα

　　cot(2π-α)=-cotα

    诱导公式六

　　π/2±α及3π/2±α与α的三角函数值之间的关系：

　　sin(π/2 α)=cosα

　　cos(π/2 α)=-sinα

　　tan(π/2 α)=-cotα

　　cot(π/2 α)=-tanα

　　sin(π/2-α)=cosα

　　cos(π/2-α)=sinα

　　tan(π/2-α)=cotα

　　cot(π/2-α)=tanα

　　sin(3π/2 α)=-cosα

　　cos(3π/2 α)=sinα

　　tan(3π/2 α)=-cotα

　　cot(3π/2 α)=-tanα

　　sin(3π/2-α)=-cosα

　　cos(3π/2-α)=-sinα

　　tan(3π/2-α)=cotα

　　cot(3π/2-α)=tanα  　　(k∈Z)

5.两角和与差的正弦、余弦、正切公式和二倍角公式

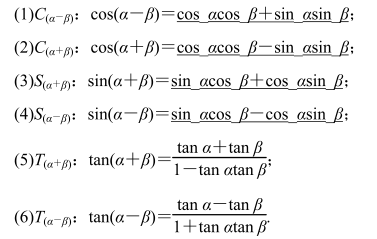
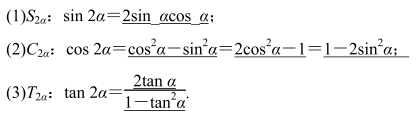
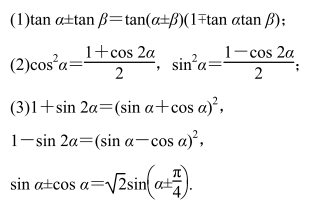
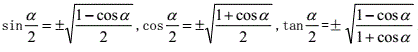
6.万能公式、和差化积公式、积化和差公式

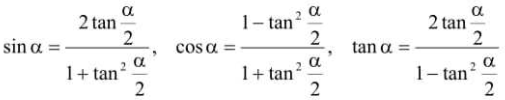
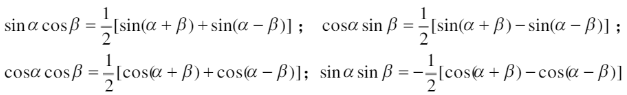
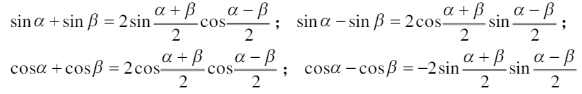
7.正弦定理、余弦定理